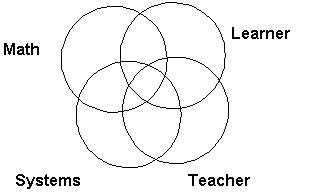
A wonderful discussion on the AMTE Listserv concerning Math Methods courses began last spring and continued through the fall semester. Many issues were raised and discussed, and I was asked to write a short article concerning the many dilemmas that so many of us agonize over as we plan for and teach these courses. I want to focus primarily on the dilemma of what to "uncover"1 in the Methods course. Pat Thompson, Ginny Keen and others were helpful in causing us to take pause with the words we use. It reminds me how easy it is to use words without carefully thinking about what they mean, e.g., constructivism, understand, conceptual understanding, etc. When I think of the many things to be included in a Methods course, the following diagram is helpful. That is, in order to teach effectively, a teacher must have and be able to apply knowledge of: mathematics, learners, pedagogy, and systems (e.g., 40 minute periods, letter grades, etc.) For me, one of the goals of a Methods course is to help the students to develop, or refine, a mindset for how to think about these four aspects and how they interact.

That this is a non-trivial task is obvious; how to pull it off is not. I was talking to a colleague who, like me, teaches both math content courses and methods courses, and we discovered that we both find the content courses much "easier" than the methods courses. Various authors have phrased this complexity in different language. I offer the following; in a Methods course, there are three highly interrelated conversations that need to happen and be connected: talking about math, talking about how children learn math, and talking about how to "teach" children to learn math.
In the Listserv discussions, there was strong consensus that most students entering a methods course do not have sufficient math knowledge to teach the course and this is not just true for elementary but also middle and secondary students.2 Thus, spending time on mathematics in a Methods course is something that most of the respondents mentioned doing. However, this decision opens up a host of issues that need to be addressed. I will articulate two here. One, few students enter a Methods course expecting to have a lot of emphasis on learning mathematics--"hey we already know this stuff; teach us how to teach," thus, the teacher must attend to maladaptive beliefs and attitudes, both about mathematics and about teaching. Two, there is growing evidence that limitations in mathematical knowledge are not only real but are be very limiting. Sharing his own research, Randolph Philipp stated that "We learned that one of the major issues that affected the extent to which our students were able to understand their children's mathematical thinking was their own understanding of the mathematics." Pat Thompson argued for taking care about what we focus on: "By focusing on what people understand [as opposed to what they don't understand], we become clearer about understandings we want them to have, and that allows us to be clearer about how we might help them move from where they are to where we insist they be in order that they be allowed to teach."
I know that I have not begun to capture the many important issues that were raised and topics that were discussed. If you do not subscribe to the Listserv, hopefully this has whetted your appetite. I will re-ask a question that I asked in July: Which subset of important questions would be most productive for me to have my students grapple with during the 14 weeks I have with them? Here are a few of the ones that I wrestle with. Of course, focusing on any of these questions then uncovers (unleashes) a whole host of more specific questions!
After teaching Methods courses for 10 years now, I am more and more leaning toward Alfred North Whitehead's advice in the still relevant The Aims of Education: "Do not teach too many subjects," and again, "What you teach, teach thoroughly."3Therefore, I am coming to believe that I serve my students better if we pursue fewer questions in more depth.
2 Note that here, a wonderful discussion could be had on this one area--how do we know this, what do we mean by understand, etc.
3 Macmillan Publishing Company, p. 2. [Copyright is 1927, the book I cite was published in 1967.]
[ Top of Document ] [ Back to index ]