Use of a Question Formulation Technique (QFT) to Engage Students in Mathematical Inquiry

Introduction

Given the stay-at-home order and virtually teaching students during the pandemic, I tried to engage my students in mathematical inquiry via Zoom. What does such inquiry look like in an online environment? What research-based practices prove helpful? Below, I share a vignette of what happened in my undergraduate STEM course, and reflect on how I could have improved student learning and engagement through the Question Formulation Technique (QFT).

Problems of Practice

As noted above, I was teaching an undergraduate STEM course via Zoom to elementary education sophomores. We were discussing speed and motion. At one point in the lesson, I presented a picture in which a camper walked 1000 meters across a flat campground and marked her path by dropping one stone every minute. Some stones were closer together and some were farther apart. The students were asked to say something about how fast the camper was walking. The sound of silence was deafening. So, I started asking questions to ostensibly evoke some thinking. “So, picture yourself walking, skipping, and running across campus and dropping a stone every minute. What would account for some stones falling next to each other and others spaced farther apart?” I did my requisite wait time and eventually one student said, “When the stones are closer together, she is moving fast.” I replied, “What makes you say that?” We eventually got through this lesson, but it was painful. Then, the lesson presented three different graphs that depicted a girl walking from camp to a van and back to camp. The students were asked to determine which graph accurately depicted the camper’s travel (see graphs below). Again, silence prevailed. After some uncomfortable wait time, I again posed a question. This questioning and prodding went on far too long as I tried to drag out responses. Abject despair covered my screen. Obviously, my instructional strategy needed repair! I am glad to report that the strategy discussed below has resulted in less despair, wait time, and dead silence!

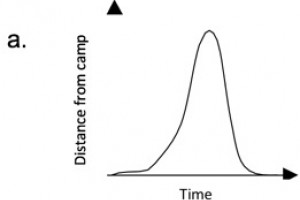
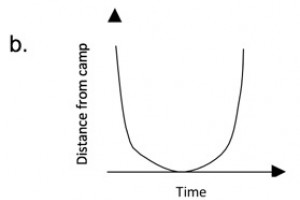
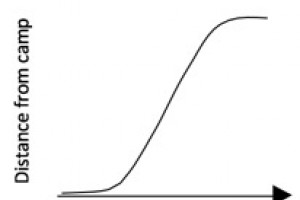
SOURCE: Graphs from Videocases for Sciences Teaching Analysis (ViSTA): Force and Motion. Copyright © 2011 by BSCS. All rights reserved. Used with permission.

A Change in Practice

The now classic book, Make Just One Change: Teach Students to Ask Their Own Questions, by Rothstein and Santana (2011) encourages teachers to adopt the Question Formulation Technique (QFT) as a routine practice. In the mathematics classroom, the QFT offers a number of benefits such as a way to recruit all student voices in the exploration of a problem, engender a growth mindset, build sensemaking, and create critical conversations and discourse. The QFT can also be used as a formative assessment to gain insight about student thinking, conceptual understanding, and problem-solving strategies.

The authors assert that QFT promotes “three wise thinking abilities” (p. 15). These three abilities of thinking are divergent thinking, convergent thinking, and metacognition. Divergent thinkers generate creative ideas, make inquiries, offer multiple solutions to problems, and explore new possibilities; whereas, convergent thinkers consolidate information, connect the dots, and solve the puzzle. Both kinds of thinking are needed to engage in highly creative and successful endeavors. Metacognition is customarily defined as the ability to think about one’s own thinking, learning, and doing. It is an internal self-monitoring and questioning process that does not come naturally to students and requires intentional instruction through strategies such as think-aloud protocols (see How People Learn II, 2018). Rothstein and Santana claim that the integration of the QFT protocol into classroom practice will greatly enhance student acquisition of these three thinking abilities and provide students with a powerful method to promote deeper inquiry and learning.

Many teachers advocate that the QFT process works best with small groups of students in which one student serves as the scribe for the group. Setting a time limit for each step is necessary to keep the process flowing. Most protocols take about thirty to forty-five minutes of class time. 

The initial step in using the QFT is to choose a Question Focus (QFocus). For mathematics, the focus can consist of a word problem, a graph, an equation, a design challenge, etc. The prompt or focus must attract student attention, promote inquiry, and be ripe for reflection and questioning. Once the QFocus is presented, the teacher reviews the overarching rules that govern the QFT protocol. These rules are meant to free the teacher from offering assistance to the students.

1. Ask as many questions as you can.

2. Do not stop to discuss, judge, or answer any of the questions.

3. Write down every question exactly as it was stated.

4. Change any statements into questions (Rothstein and Santana, p. 19).

Once the rules are explained, the teacher asks the students to think again about the QFocus and generate as many questions as they can. Once a sufficient number of questions are created, the teacher works through the remaining steps. These steps require the students to categorize all of their questions as open and closed; change an open question to a closed one and vice versa; cite advantages and disadvantages of open and closed questions; improve their questions; prioritize them; use the questions to address the teacher’s learning goals; and, reflect on what the students learned, how their thinking evolved, and what insights were gained.

In order to help the students understand the process of asking questions, the teacher engages the students in ongoing reflective conversations. For example, the teacher may ask the students about the purpose of open and closed questions, or why prioritizing questions is important. Exploring these connections is tricky because the teacher must refrain from asking questions or helping students formulate questions. The authors note facilitating the QFT is both an art and a science. Many teachers concur with the authors by observing that the reflection at the end of the protocol requires deft and skillful management. Teachers are striving to help students think about how their questions reveal greater understanding of the topic or focus and how they plan to use their questions to make sense of the phenomenon. Finally, as you might be able to tell, facets of divergent, convergent, and metacognitive thinking permeate the QFT protocol.

Pedagogy Redux

Let’s reframe the opening STEM experience that I described and think about how the QFT could have been used as a formative assessment. That is, a way for me to understand student thinking, and an opportunity for them to have time to process the question, draw parallels from the “dropping stones” problem, and interpret the graphs. A more productive approach would have been to present the graphs as the QFocus after we had some discussion about the stones picture. After a brief introduction to the purpose and rules of the QFT, students could have been placed in breakout rooms to generate an initial set of questions. Once back in the main room, groups could have shared their questions. These questions would have revealed insights into their current conceptual understanding. As groups continued the steps of the QFT protocol, the refining and prioritizing of the questions would have offered a developmental picture of what they were thinking about the problem and how they were using the questions to make sense of the task. In a sense, assessment is playing out live in the classroom, and the ongoing discussion provides opportunities for each group to assess their own thinking against that of others.  

As I reflected on revising my problem of practice, I wondered about the technology tools necessary to facilitate the QFT. The tool would need to be easy to use, accessible, flexible, collaborative, and sharable. Immediately, Padlet (Padlet) appears to be the tool of choice due to its flexible format, editable and moveable posts, shareable use, and audio for accessibility. However, the free version only allows three boards. Alternatives to Padlet are Lino, Pinside, Wakelet and Scrumblr. These alternatives are primarily sticky note based boards but free to teachers at this time. Other tools to consider include Google docs and slides, and digital whiteboards included in most online platforms such as Zoom or Canvas.

As seen in this vignette, the QFT offers a significant change in practice that sharpens the focus of the lesson, provides a scaffolded approach to support student inquiry, and transfers the responsibility for that inquiry to students. In the long run, students will develop a unique habit of mind that will serve them well across many domains.

Author’s note/tip: A number of resources exist to support the use of the QFT in K-12 and higher education.

The text by Rothstein and Santana is a good place to start but the original work is resourced at the Right Question Institute (RQI) (https://rightquestion.org/). The RQI provides QFT templates, videos, and stories from teachers about using the QFT. One resource for math teachers is located at https://rightquestion.org/resources/qft-in-math/

Also, if you sign up on the RQI site, you will receive alerts about recent posts from teachers and professors throughout the world and invitations to workshops and webinars. I recently participated in an online QFT workshop in which we generated questions to guide a research topic of interest. Not only did the workshop help hone my QFT skills in an online environment, but it also connected me to an international community of practice which has already proved valuable. Please reach out to Andrew Minigan at Andrew.Minigan@rightquestion.org for more information.

References:

BSCS. (2011). Videocases for Sciences Teaching Analysis (ViSTA): Force and Motion. Retrieved from https://bscs.instructure.com/courses/285/pages/fm-home

National Academies of Sciences, Engineering, and Medicine. (2018). How People Learn II: Learners, Contexts, and Cultures. Washington, DC: The National Academies Press. doi:https://doi.org/10.17226/24783.

Rothstein, Dan, and Luz Santana. (2011). Make Just One Change: Teach Students to Ask Their Own Questions. Cambridge, MA: Harvard Education Press.