Standard C.1. Mathematics Concepts, Practices, and Curriculum
|
Well-prepared beginning teachers of mathematics possess robust knowledge of mathematical and statistical concepts that underlie what they encounter in teaching. They engage in appropriate mathematical and statistical practices and support their students in doing the same. They can read, analyze, and discuss curriculum, assessment, and standards documents as well as students’ mathematical productions. |
C.1.1. Know Relevant Mathematical Content C.1.2. Demonstrate Mathematical Practices and Processes C.1.3. Exhibit Productive Mathematical Dispositions C.1.4. Analyze the Mathematical Content of Curriculum |
Effective teachers have deep understandings of the mathematics they are expected to teach and exhibit positive dispositions toward both mathematics teaching and learning. Such understandings and dispositions are particularly critical for upper elementary teachers because they develop the foundations of mathematical understanding, beliefs, and attitudes among young learners to start students on their mathematical journeys. Therefore, we have a critical elaboration of this standard for the preparation of teachers of mathematics in upper elementary grades.
UE.1. Mathematics Concepts and Connections to Mathematical Practices
Well-prepared beginning teachers of mathematics at the upper elementary level understand foundational mathematics concepts that they will teach, and they connect those concepts to mathematical practices as well as to the mathematics of Pre-K–2 and the middle level curriculum. [Elaboration of C.1.1 and C.1.2]
Prospective upper elementary grade teachers often enter their preservice teacher education courses with fragile mathematics identities. Many of them voice concerns about teaching mathematics because of their own, often negative, mathematics instructional experiences in Pre-K–16 education. Or, they may feel a sense of relief because they believe that learning elementary mathematics means knowing how to compute with the basic operations. They may think that because they know how to multiply, they can teach multiplication. Within elementary mathematics concepts are depth and complexity that candidates can and must understand. Even though the standard algorithms often continue to be emphasized in elementary schools, candidates may not know that the familiar algorithms that they learned in school and often used without understanding can and often are taught by linking these procedures to important mathematical structures and properties. Thus, developing the foundations of a robust mathematical-knowledge base is essential for learning how to effectively teach elementary mathematics.
Even well-prepared beginners do not learn all the mathematics content they need to teach all elementary grade levels in their preservice teacher education programs. However, they must study some key areas, and they should have opportunities to study some of these in depth. Key areas for upper elementary candidates include base-ten numbers, multiplicative structures, fractions and decimals, algebraic thinking, measurement, and geometry.
In brief summaries below, we describe the significant concepts that well-prepared beginning teachers of mathematics must know to be able to support learners in upper elementary grades and how those concepts connect with mathematical practices. The summaries include specific, but not exhaustive, examples of what is involved in understanding and being ready to teach this content. These ideas connect to and reflect the MET II content expectations (CBMS, 2012) and, therefore, we include the related MET II content expectations in each section in addition to content identified in research in mathematics teacher education. This section was also influenced by representations of core understandings found in documents such as NCTM’s Developing Essential Understandings series (cf. Clark et al., 2010), Curriculum Focal Points (Schielack, et al., 2006), and the Common Core State Standards – Mathematics (NGA & CCSSO, 2010).
Multiplicative Structures. Well-prepared beginning teachers of mathematics in the upper elementary grades are multiplicative thinkers, with deep understandings of the following concepts and topics:
- Multiplication and division have meaning, including several interpretations, and involve more than just memorization of basic facts and procedures. Sometimes teachers (and students) believe that multiplication is merely repeated addition or equal groups and that division is only making groups, but well-prepared beginning teachers must be familiar, beyond those partial understandings, with the multiple mathematical meanings of and real-world contexts for multiplication and division. Well-prepared beginning teachers can represent these operations in many ways and can make connections between representations and problem types.
- Properties, such as the commutative, associative, and distributive properties, support justification, flexibility, and fluency and help students make sense of multi-digit computation.
- Computation involving multiplication and division includes mental computation, estimation strategies, invented algorithms, and standard algorithms (Otto, Caldwell, Lubinski, & Hancock, 2011).
Well-prepared beginning teachers of the upper elementary grades must understand the concepts of multiplication and division, including multiple representations of the concepts as well as how to sequence and teach this content to students. Teachers recognize the relationships between the content that precedes multiplication and division (e.g., addition, subtraction, and place value) and the content that follows multiplication and division (e.g., ratios and proportions). The movement from additive thinking, particularly counting by ones, to multiplicative thinking or seeing an equal group as a unit is challenging for students, and the well-prepared beginning teacher predicts and responds to that potential barrier.
Well-prepared beginners know that the way to approach this content is through engaging students in reasoning about situations involving multiplication and division. Such activities present opportunities to connect the action described in the problem with the arithmetical operations, which is also essentially the definition of the mathematical practice of making sense of problem situations. Well-prepared beginners know how to select and sequence problems to introduce students to a range of interpretations of these concepts and to the need to develop strategies for solving these problems through multiple approaches. These approaches include skip counting, equal groups, area and array models, multiplicative comparisons, ratio tables, scaling, and partitive- and measurement-division situations (Otto, Caldwell, Lubinski, & Hancock, 2011). Additionally, well-prepared beginners are able to select rich tasks that lead students to the use of multiple approaches, connect to relevant contexts, and connect to other content within mathematics.
Table 5.2 lists MET II report (CBMS, 2012) items related to multiplicative structures in the upper elementary grades.
Table 5.2. Connections to MET II (CBMS, 2012) Related to Multiplicative Structures in the Upper Elementary Grades
MET II describes the following essential ideas related to multiplicative structures:
- “The different types of problems solved by multiplication and division, and meanings of the operations illustrated by these problem types.
- Teaching–learning paths for single-digit multiplication and associated division, including the use of properties of operations (i.e., the field axioms).” (p. 26)
- “Recognizing that addition, subtraction, multiplication, and division problem types and associated meanings for the operations (e.g., CCSS, pp. 88–89) extend from whole numbers to fractions.” (p. 28)
Fractions and Decimals. Well-prepared beginning teachers of mathematics at the upper elementary level have strong understandings of fractions and decimals, including the following concepts and topics:
- Fractions have multiple interpretations, including part-whole relationships, measures, quotients, ratios, and operators.
- The unit is a foundational concept, “fundamental to the interpretation of rational numbers” (Otto et al., 2011, p. 8).
- Equivalence is a key concept. Fractions can be expressed in an infinite number of equivalent fractions and in decimal form.
- Understanding the magnitudes of fractions and decimals enables students to compare and order these numbers and perform computational estimation.
- Computation with fractions and decimals builds on understanding of whole number operations, but some interpretations and contexts make more sense than others. Estimation and mental arithmetic continue to be important.
Students in upper elementary grades experience shifts in their mathematical thinking that include
- Shifting from discrete, countable quantities only to include continuous quantities.
- Shifting from one model to a variety of representations, flexibly thinking about the unit.
- Shifting from whole-number-based comparisons to equivalence-based comparisons
- Shifting from rules to making sense about operations on fractions (Otto et al., 2011).
When students experience the natural disequilibrium the occurs when making these shifts, well-prepared beginners are ready to support sense making and understanding. This is a context in which an explicit emphasis on mathematical practices can play a key role. Well-prepared beginners encourage students to communicate their reasoning, critique the reasoning of others, and develop arguments through discourse and mathematical writing. Beginning at the third grade, students will learn that an argument is a carefully crafted sequence of statements and that reasoning strategies are presented with an objective to convincing others that a claim is true or false, rather than being merely a written listing of procedural steps taken in a process or algorithm used to arrive at an answer. Students in upper elementary grades are formally introduced to mathematical argument, including a claim, justification of the claim with evidence, and warrants that connect the reasoning and evidence to the claim (Casa et al., 2016). This introduction helps set the foundation for mathematical arguments in later grades, including inductive and deductive proof and the analysis, representing, reasoning, revising, and reporting demands of mathematical modeling at the high school level.
Table 5.3 lists MET II report (CBMS, 2012) items related to fractions and decimals in the upper elementary grades.
Table 5.3. Connections to MET II (CBMS, 2012) Related to Fractions and Decimals in the Upper Elementary Grades
MET II describes the following essential ideas related to fractions and decimals:
- “Understanding fractions as numbers that can be represented with lengths and on number lines. Using the CCSS development of fractions to define fractions
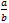 as a parts, each of size
as a parts, each of size 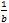 . Attending closely to the whole (referent unit) while solving problems and explaining solutions.
. Attending closely to the whole (referent unit) while solving problems and explaining solutions. - Recognizing that addition, subtraction, multiplication, and division problem types and associated meanings for the operations (e.g., CCSS, pp. 88–89) extend from whole numbers to fractions.
- Explaining the rationale behind equivalent fractions and procedures for adding, subtracting, multiplying, and dividing fractions. (This includes connections to grades 6–8 mathematics.)
- Understanding the connection between fractions and division,
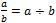 , and how fractions, ratios, and rates are connected via unit rates. (This includes connections to grades 6–8 mathematics. See the Ratio and Proportion Progression for a discussion of unit rate.)” (p. 28)
, and how fractions, ratios, and rates are connected via unit rates. (This includes connections to grades 6–8 mathematics. See the Ratio and Proportion Progression for a discussion of unit rate.)” (p. 28) - “Extending the base-ten system to decimals and viewing decimals as address systems on number lines. Explaining the rationales for decimal computation methods. (This includes connections to grades 6–8 mathematics.)” (p. 27)
Geometry and Measurement. Well-prepared beginning teachers of mathematics at the upper elementary level have strong understandings of geometry and measurement. They understand core measurement concepts such as iteration, conservation, and origin and provide frameworks for connecting linear measurement with measures of area and volume (Clements & Sarama, 2014). They can make correspondences between direct measurement of properties of shapes and algebraic approaches to determine the same measures. They can harness ideas such as line symmetry and reflection to solve problems and as tools for thinking about fractions, area, and proportions. Lehrer and Slovin (2014) noted the importance of understanding that
- “Transforming objects and the space that they occupy in various ways while noting what does and does not change provides insight into and understanding of the objects and space.” (p. 8)
- Measuring attributes is one way to analyze and describe geometric shapes.
- Classifying properties of objects helps one investigate relationships between types of objects.
Well-prepared beginning teachers of mathematics at the upper elementary level can engage meaningfully in these mathematical topic areas through the mathematical practices. For example, these teachers are not only able to use measurement tools and construct figures but are also skilled in describing how to select appropriate tools. They know how to highlight the decision-making process for students, explaining how tools are used to provide accurate information. For example, well-prepared beginners in the upper elementary grades know how to use a protractor and also know how to talk about and show the use of this measuring tool in such a way that they could help students work through the array of challenges that often arise when using a protractor. Vignette[1] 5.1 showcases struggles that students sometimes face when learning to measure angles.
Vignette 5.1. Measuring Angles
Ms. Hernandez is watching her students use protractors to measure a variety of angles. On a seating chart, she records what she observes small groups of students doing and key points she hears them discussing. She also sketches what the students’ protractors look like in relation to the angle being measured. Some of the information she records includes the following:
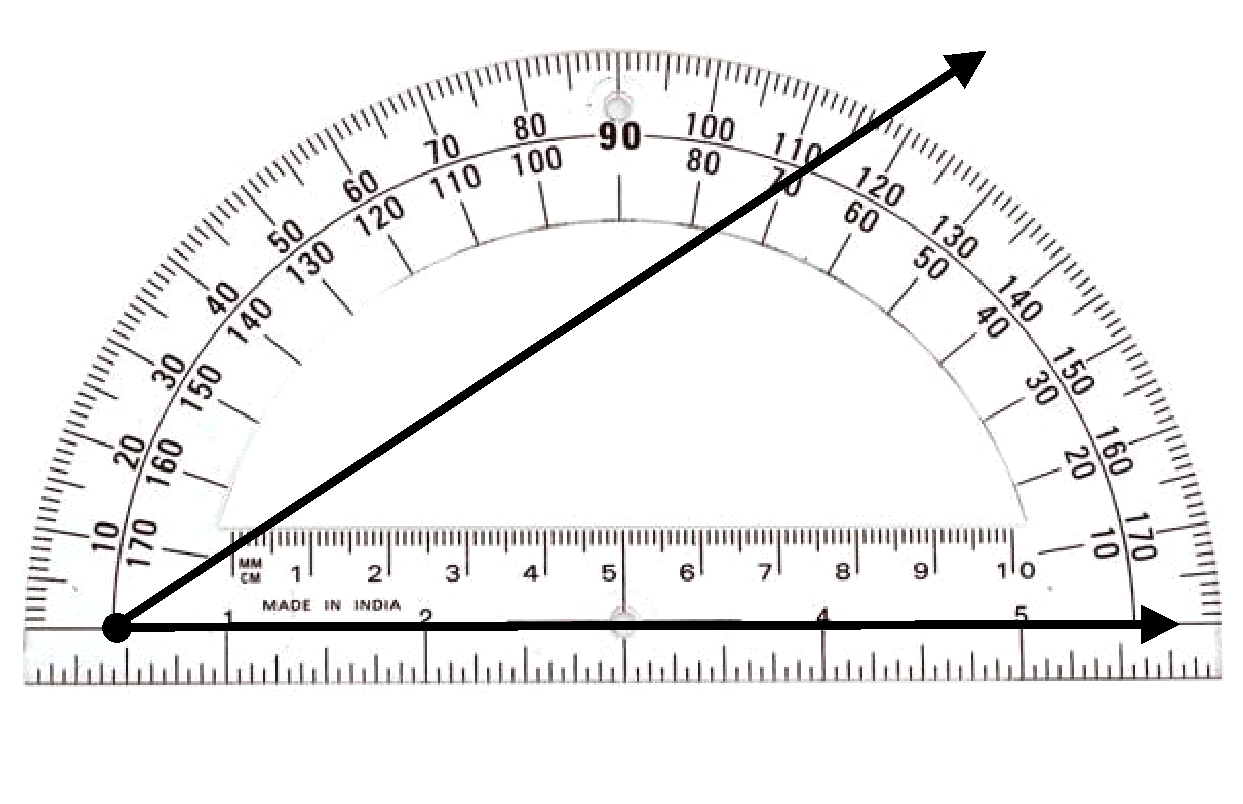
Group 1, Donte: “We are doing everything right, but now there are two numbers, 20 and 160, on the protractor. Which number do we use?” (see image below)
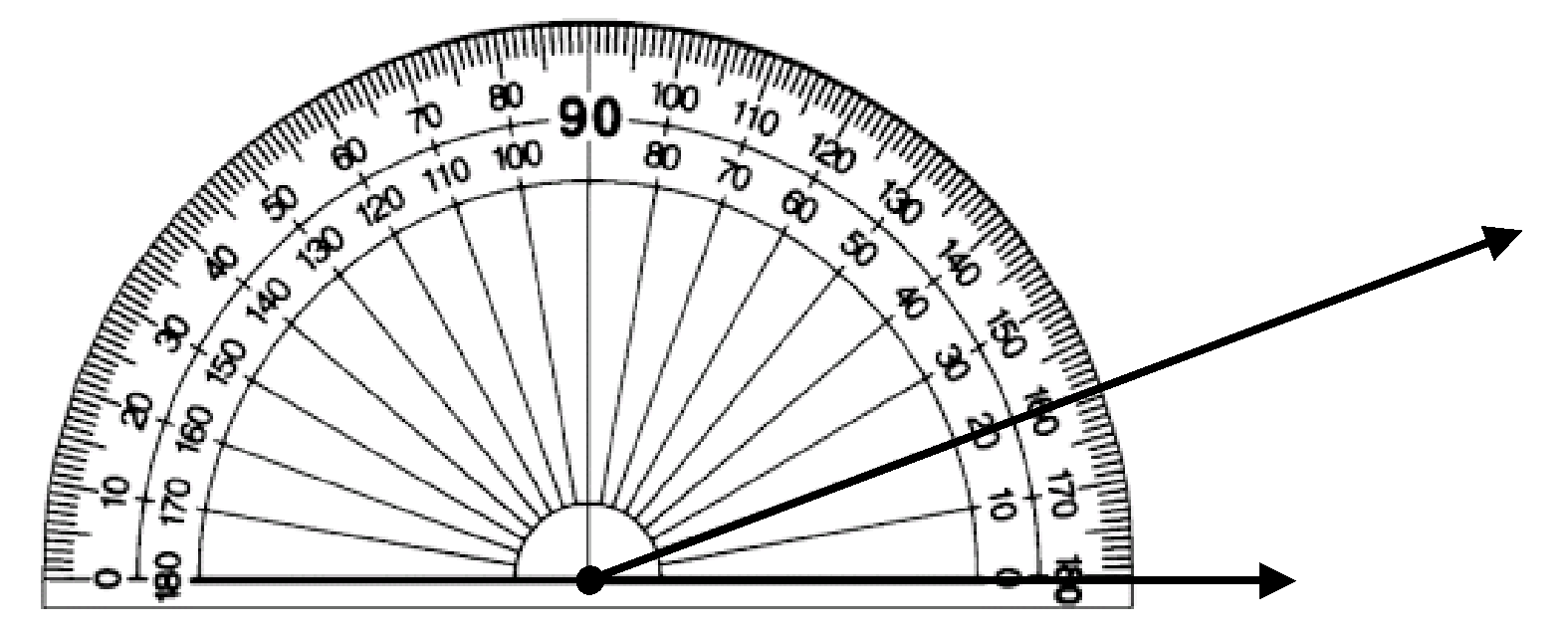
Group 2, Armando, speaking to Group 1: “Move your protractor and just look at the angle. Is it bigger or smaller than a square corner? If the angle is smaller, you pick the smaller number because a square corner is 90 degrees.”
Group 3, Vince: “Where are you supposed to put the little circle?” J’La: “You put it where both of the arrows start.”
Group 4, Maribel: “When I put the protractor on the bottom arrow, I get 5 inches. Is that how long the angle is?” (see image below).
Group 5, Cristina: “This angle is too short to measure. The lines don’t reach the numbers on the protractor”. Diego draws the line from the angle to the scale on the protractor and says, “See, you just make the sides long enough to get to the numbers.”
Ms. Hernandez anticipated many of the challenges her students encountered and wants them to collectively make sense of how to effectively use the protractor. Using her notes, she lists the students' questions and big ideas on the front board. Then, from her observations, she tentatively plans whom she will ask to share in the whole-class discussion; she will include students who present challenges for the class to think about and also students she could strategically call on to contribute ways of thinking that could move the discussion forward. She is ready to assist students in using the document camera to show how the protractor and angle looked in different situations, to support the precise use of mathematical language, and to involve many students to build on, question, and critique what is said.
Another example of well-prepared beginners’ use of mathematical practices in this area is through the ways in which they are able to attend to precision. They know the affordances of referring to a square as a rectangle, rhombus, parallelogram, or quadrilateral and can generate contexts that require measurement of time to the nearest hour, minute, or tenth of a second. The well-prepared beginner also knows that decisions about precision will affect the selection and use of particular tools or representations. For example, if one is measuring to the nearest inch, she has no real need to use a ruler partitioned to show 16ths-of-an-inch increments. If weighing a very light object in a science experiment, one needs something more sensitive than a bathroom scale.
Table 5.4 lists items from the MET II report (CBMS, 2012) related to geometry and measurement in the upper elementary grades.
Table 5.4. Connections to MET II (CBMS, 2012) Related to Geometry and Measurement in the Upper Elementary Grades
MET II describes the following essential ideas related to geometry and measurement:
- “Understanding geometric concepts of angle, parallel, and perpendicular, and using them in describing and defining shapes; describing and reasoning about spatial locations (including the coordinate plane).
- Classifying shapes into categories and reasoning to explain relationships among the categories.
- Reason about proportional relationships in scaling shapes up and down.” (p. 30)
- “The general principles of measurement, the process of iterations, and the central role of units: that measurement requires a choice of measureable attribute, that measurement is comparison with a unit and how the size of a unit affects measurements, and the iteration, additivity, and invariance used in determining measurements.
- How the number line connects measurement with number through length…
- Understanding what area and volume are and giving rationales for area and volume formulas that can be obtained by finitely many compositions and decompositions of unit squares or unit cubes, including formulas for the areas of rectangles, triangles, and parallelograms, and volumes of rectangular prisms...
- Using data displays to ask and answer questions about data. Understanding measures used to summarize data, including the mean, median, interquartile range, and mean absolute deviation, and using these measures to compare data sets.” (p. 29)
Algebraic Thinking. Well-prepared beginning teachers of mathematics at the upper elementary level have strong understandings of algebraic thinking, including the following concepts and topics (Blanton, Levi, Crites, & Dougherty, 2011):
- The fundamental properties of arithmetic, such as the commutative, associative, and distributive properties, also hold for algebra.
- Equations represent an equivalent relationship.
- Variables can be used to describe mathematical ideas and may have different meanings.
- Quantitative reasoning helps one make generalizations about relationships.
Well-prepared beginners understand students' intuitive strategies and how those strategies build on and connect with the properties of operations and other algebraic concepts (Carpenter, Franke, & Levi, 2003). They fluently use mathematical symbols and conventions to express mathematical ideas. They can readily translate and contextualize symbolic representations of phenomena as well as notice mathematical relations and patterns within real-life and problem contexts that can be expressed more generally or abstractly. They are well positioned to help students engage in mathematical practices in which thinking quantitatively is linked with opportunities to reason abstractly. Representations such as drawings, schemas, and equations are vehicles that students can use to carry their thinking into more abstract realms. While maturing, upper-elementary-grade students are increasingly able to record their thinking, so beginning teachers make the recording of thinking and reasoning an integral part of instruction and assessments at these grade levels.
Well-prepared beginners make connections between algebraic representations and graphs and tables of the same situations as well as discuss the relative advantages of different representations. They use graphs and tables to give meaning to algebraic expressions and can draw students’ attention to the elegance and power of an algebraic expression to model the mathematics of a situation. They know when and how an algebraic representation can be used both to capture the logic of a numerical pattern and to show the mathematical structure of a situation.
Table 5.5 lists items from the MET II report (CBMS, 2012) related to algebraic thinking in the upper elementary grades.
Table 5.5. Connections to MET II (CBMS, 2012) Related to Algebraic Thinking in the Upper Elementary Grades
MET II describes the following essential idea related to algebraic thinking:
- “Recognizing the foundations of algebra in elementary mathematics, including understanding the equal sign as meaning ‘the same amount as’ rather than a ‘calculate the answer’ symbol.” (p. 26)
[1] This chapter includes vignettes meant to bring to life the recommendations. The vignettes serve a number of purposes, including proposing tasks that may be used with candidates for particular purposes, providing example interactions from mathematics or mathematics methods courses to exemplify effective instruction, and describing the experiences of a teacher candidate. Each vignette was chosen to highlight a particular point, but use of an isolated vignette may require surrounding context to preserve the spirit intended in the use.
