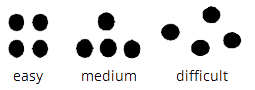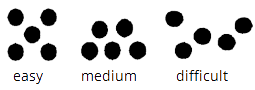EC.3. Mathematics Learning Trajectories: Paths for Excellence and Equity
Well-prepared beginning teachers of mathematics at the early childhood level understand learning trajectories for key mathematical topics, including how these learning trajectories connect to foundational knowledge, curriculum, and assessment frameworks. [Elaboration of C.1.4]
Learning trajectories are effective frameworks to use in developing foundations of early mathematics. They are especially important in early childhood for six reasons (Clements & Sarama, 2014). First, children’s cognitive development influences how they think and what they can learn about mathematics, arguably, more in these early years than at any other age. Often the variance among children on a variety of cognitive factors is also particularly wide at this level. Second, contexts for teaching (e.g., whole group, learning centers, small groups, individual interactions, informal settings) are varied in early childhood and difficult to coordinate and use for helping children learn mathematics without a teacher's holding a good understanding of learning trajectories. Third, the younger the children the greater the importance of teachers' using children’s thinking and prior knowledge as starting points. Fourth, much is known about learning trajectories in early mathematics, arguably more than for any other age range (see Table 4.5 for a listing of current research-based learning trajectories). Fifth, despite these reasons, most teachers of young children do not understand or use these learning trajectories. For example, in one study (Supovitz, Ebby, & Sirinides, 2013), only 3% interpreted children’s responses at the conceptual level and none at the highest level of the learning trajectories, and more than 3/4 of the teachers suggested only procedural instruction. Sixth, research and developmental work indicate that learning trajectories are effective guides for informing instructional approaches that support young children’s learning of mathematics. They also help early childhood educators respect children’s developmental processes and constraints as well as their potentials for thinking about and understanding mathematical ideas.
Table 4.5. Research-based Developmental Learning Trajectories
- Recognition of Number and Subitizing
- Verbal and Object Counting
- Comparing, Ordering, and Estimating Numbers
- Early Addition and Subtraction
- Composing Number and Multidigit Addition and Subtraction
- Early Multiplication and Division and Fractions
- Spatial Thinking
- Shapes
- Composition of 3D Shapes
- Composition and Decomposition of 2D Shapes
- Length Measurement
- Area Measurement
- Volume Measurement
- Angle Size
Note. See Clements and Sarama, 2014, and Sarama and Clements, 2009, for detail on each of these trajectories.
Each learning trajectory has three components: a mathematical goal, a developmental progression, and instructional strategies (Sarama & Clements, 2009). To develop a particular mathematical understanding (the goal), children construct each level of thinking and reasoning sequentially (the developmental progression), if provided with appropriate teaching approaches and tasks (the instructional strategies). Prospective early childhood teachers need to learn that these components are intimately and intrinsically interconnected in high-quality instruction. That is, the key to true understanding and successful use of learning trajectories lies not in understanding just each component but in understanding how the components work together and must be used in concert to engage and support young children’s learning and thinking about mathematics. This understanding is a demanding expectation, and, thus, we recommend that candidates study in depth at least three research-based developmental learning trajectories. For example, candidates might study learning trajectories for subitizing (shown in Figure 4.1), early adding and subtracting, and length measurement. This in-depth study would include instructional planning and application of all three integrated components for each learning trajectory examined, thus serving as a model for utilization of other development trajectories. In addition, candidates should become familiar with other developmental learning trajectories for early mathematics, including how to find resources to extend their own knowledge and support eventual implementation in their own classrooms.
Goal
The goal connects learning trajectories to the important big ideas in mathematics. The relevant big idea is that numbers can be used to tell how many, describe order, and measure; they involve numerous relations and can be represented in various ways. The specific goals include understanding that subitizing can be used to tell how many (perceptual subitizing), that a quantity can consist of parts and can be broken apart (decomposed) into the parts, and that those parts can be combined (composed) to form the whole (conceptual subitizing). Specific objectives are for children to achieve those understandings and fluency in perceptual and conceptual subitizing.
|
Age (yrs) |
Developmental Progression |
Sample Instructional Tasks |
|---|---|---|
|
0–1 |
Pre-Explicit Number. Within the first year, the child is sensitive to small numbers, but does not have explicit, intentional knowledge of number. |
Noticing Collections. Provide a rich sensory environment, use words such as more, and use actions of adding objects. |
|
1–2 |
Small-Collection Namer. Names groups of 1 to 2, sometimes 3. Shown a pair of shoes, says, “Two shoes.” |
Board Games–Small Numbers. Play board games with a special die (number cube) or spinner that shows only 1, 2, and 3 dots (then add 0 to it). |
|
3 |
Maker of Small Collections. Nonverbally makes a small collection (no more than 4, usually 1–3) with the same number as another collection via mental model (i.e., not necessarily by matching). Might also be verbal. When shown a collection of 3, makes another collection of 3. |
Get the Number. Ask children to get the right number of crackers or some other item for a small number of children. |
|
4 |
Perceptual Subitizer to 4. Instantly recognizes collections up to 4 briefly shown, and verbally names the number of items. When shown objects briefly, says, “Four.” |
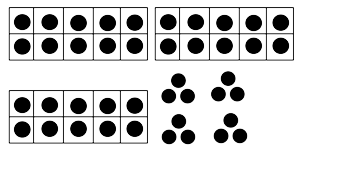
Snapshots. Play "Snapshots" with collections of one to four objects, arranged in line or other simple arrangement, asking children to respond verbally with the number name. Start with the smaller quantities and easier arrangements, moving to those of moderate difficulty only when children are fully competent and confident.
easy medium difficult |
|
5 |
Perceptual Subitizer to 5. Instantly recognizes briefly shown collections up to 5 items and verbally names the number of items. Recognizes and uses spatial and numeric structures beyond the situations in which they were already experienced. Shown 5 objects briefly, says, “Five.” |
Snapshots: Play "Snapshots" with dot cards, starting with easy arrangements, moving to more difficult arrangements when children are able to do so.
easy medium difficult |
|
5 |
Conceptual Subitizer to 5. Verbally labels all arrangements to about 5, when shown only briefly. Asked "Why?” says, “Because I saw 3 and 2, and so I said 5.” |
Snapshots. Use different arrangements of the various modifications of “Snapshots” to develop conceptual subitizing and ideas about addition and subtraction. The goal is to encourage children to see the addends and the sum.
|
|
5 |
Conceptual Subitizer to 10. Verbally labels most briefly shown arrangements to 6, then up to 10, using groups. “In my mind, I made two groups of 3 and one more, so 7.” |
Snapshots. Play “Snapshots” with larger quantities to develop ideas about addition and subtraction.
|
|
6 |
Conceptual Subitizer to 20. Verbally labels structured arrangements up to 20, shown only briefly, using groups. “I saw three 5s, so 5, 10, 15.” |
Ten Frame Addition Snapshots: Briefly show 2 ten frames to help children visualize addition combinations.
|
|
7 |
Conceptual Subitizer With Place Value and Skip Counting. Verbally labels structured arrangements, shown only briefly, using groups, skip counting, and place value. “I saw groups of 10s and 2s, so 10, 20, 30, 40, 42, 44,. . . 44!” |
Ten Frame Addition Snapshots. Briefly show several ten frames.
|
|
8 |
Conceptual Subitizer with Place Value and Multiplication. Verbally labels structured arrangements shown only briefly, using groups, multiplication, and place value. “I saw groups of 10s and 3s, so I thought, 3 tens is 30 and 4 threes is 12, so 42 in all.” |
Snapshots with Dots. Play “Snapshots” with structured groups that support the use of increasingly sophisticated mental strategies and operations.
|
Figure 4.1. A learning trajectory for recognition of number and subitizing.
Note. Adapted from Clements & Sarama, pp. 17–20, copyright 2014, Learning and teaching early math: The learning trajectories approach (2nd ed.) by Clements & Sarama. Adapted with permission of Taylor and Francis Group, LLC, a division of Informa plc.