EC.5 Understanding Young Children’s Mathematical Thinking Informs Teaching
Well-prepared beginning teachers of mathematics at the early childhood level elicit and analyze young children’s mathematical thinking to inform classroom interactions and instructional decisions. [Elaboration of C.2.3]
Educational assessments serve a variety of purposes. Sometimes assessments are high-stakes and are summative in nature. Other times, they serve a diagnostic function, as in the identification of children with special needs. Within the daily classroom interactions of the teacher and students, assessment is formative in nature; it guides instruction and gauges whether instruction has been effective or needs modification. Research and expert opinion (Clarke, Clarke, & Roche, 2011) indicate that the primary goal of assessing young children is to understand children’s thinking and knowledge and to inform ongoing teaching efforts. Performance tasks (meaningful activities that require children to synthesize and apply knowledge and skills by making a response or creating a product) and informal ongoing assessments such as observations, interviews/questioning sequences, paper-and-pencil tasks, computer-based tasks, and digital records (audio and video) are useful and informative ways of assessing young children’s mathematical learning and are integrated as appropriate into the early childhood mathematics curriculum.
Performing effective formative assessment supportive of early childhood learning requires that teachers understand developmental progressions of learning trajectories and set goals that are both appropriate for the children in their classrooms and responsive to each child’s learning needs. They also need to know how to assess children to identify their strengths and current levels of understanding and what levels they are likely to learn next. Vignette 4.3 illustrates such a sequence of eliciting and using children’s thinking to inform and adjust instruction. The data about children’s current thinking support the team while they collaboratively determine how the current thinking connects to the progression and ways they may support movement along the content trajectory and development of the children’s engagement with the mathematical practices.
Vignette 4.3. Collaborative Sense Making of Children’s Mathematical Thinking
The candidates in a mathematics methods course were asked to conduct a Number Talk in their classroom setting. They engaged in preplanning the Number Talk by anticipating children’s thinking and planning for how they might record their ideas using images, numbers, or both and mathematics symbols to convey the children’s thinking. Next, they reviewed the plan with their cooperating teacher (or university supervisor) who made suggestions prior to implementation and took notes about the children’s thinking during the lesson. After the lesson, they debriefed to consider next instructional steps on the basis of the thinking that emerged.
------------------------------------------------------------------------------------------------------------------------------------------------------
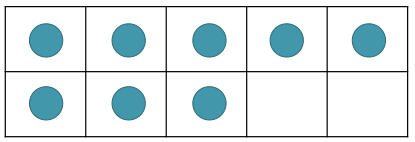
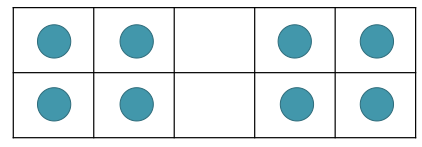
A teacher candidate in a first-grade classroom in February provided her children with images of dots in a tens frame. She was interested in having children conceptualize 8 in different ways. She also wanted to illustrate for students ways of recording their observations with words and number sentences. After meeting with her cooperating teacher, she also realized that this task would enable them both to see the extent to which children were subitizing. She planned to flash the image for 3 seconds, then again for another 3 seconds, and then discuss what children saw. After discussing the initial arrangement of dots (Formation 1), she rearranged the dots to see what else children may notice (Formation 2).
|
|
|
|
Formation 1 |
Formation 2 |
Some observations children made about Formation 1 were
- I noticed 5 on the top and 3 on the bottom.
- I counted really fast by 1s.
- I knew it was a 10 frame and there were 2 spots left. That’s 8.
- I knew a whole row is 5 then 3 more is 8.
Observations for Formation 2 were
- I noticed 4 on one side and 4 on the other. 4 + 4 = 8.
- I saw that you didn’t take any off.
- I know 2 + 2 + 2 + 2 = 8.
- It’s still the same thing.
------------------------------------------------------------------------------------------------------------------------------------------------------
When debriefing the lesson, both the candidate and cooperating teacher were impressed with the children’s thinking and participation. They decided that the Number Talk was a simple yet effective approach to gather children’s ideas even though they did not hear ideas from every child. It had helped that the candidate asked the children to show a thumbs-up signal to let her know that they understood or used the same strategy as the child sharing. The cooperating teacher pointed out that the children were subitizing to 10 and connecting their counting strategies to what they know about the operations and tenness. The candidate and cooperating teacher discussed ways that the candidate could more clearly record the children’s ideas (i.e., allowing more space to add connections, changing pen color with different ideas) and how together they could continue to develop the children’s skills with listening and making sense of others’ ideas.
The purposes of any assessment determine the content, the methods of collecting evidence, and the nature of the possible consequences for individual students, teachers, schools, or programs. Assessment that supports early childhood learning includes both formal and informal assessments and draws upon a range of sources of evidence. It enhances teachers’ powers of observation and understanding of children’s mathematical thinking, enabling them to establish individual learning goals. Strategies include individual assessment, observations, documentation of children’s talk, interviews, samples of children’s work, and performance assessments with the intent to illuminate children’s thinking, strengths, and needs.